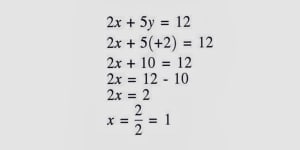
Las ecuaciones de primer grado no necesariamente tienen que ser ecuaciones de primer grado con una incógnita. Por el contrario, podemos tener varios valores desconocidos para averiguar, o pueden aparecer otros casos en donde la x esté elevada al cuadrado, dando lugar a ecuaciones de segundo grado. Hoy veremos el caso particular de las ecuaciones de primer grado donde se visualizan dos incógnitas y cómo resolver las mismas.
Este tipo de ecuaciones pueden aparecer en ejercicios de razonamiento o bien como actividad planteada. Los libros de Aurelio Baldor constan de cientos de ejercicios de ecuaciones de primer grado con dos incógnitas que puedes resolver, y puedes encontrar tanto con las ecuaciones directas así como también a través de problemas que te solicitan encontrar dos valores diferentes, como edades o cantidades, por citar ejemplos.
Un ejemplo de problema sería el caso de dos personas cuyas edades suman 50 años y se sabe que una tiene 10 años más que la otra. Podemos pensar cada edad como una incógnita distinta, y resolverla mediante lo que llamaremos sistema de ecuaciones de primer grado.
Para resolver este tipo de ecuaciones debemos plantearnos lo siguiente (continuando con el ejemplo dado):
- x + y = 50 (las edades sumadas dan 50)
- x = y + 10 (la edad de la primera persona es de 10 años más que la de la segunda)
Para resolverlas podemos optar por 3 métodos:
- Método de sustitución.
- Método de reducción.
- Método de igualación.
Empecemos con las explicaciones de modo a que aprendas cómo resolver ecuaciones de primer grado con dos incógnitas.
Método de sustitución
En este paso, la idea será aprovechar la presencia de dos ecuaciones y utilizarlas para ir hallando de a una las incógnitas. Concretamente consiste en tomar las dos ecuaciones (mismo ejemplo de antes) y expresarlas de esta manera:
- x + y = 50
- x = y + 10
Entonces, debemos encontrar una solución que verifique las dos ecuaciones. Para ello tomaremos el dato que tenemos en la segunda ya que nos dice exactamente cuanto es lo que vale x. De esta forma, sustuitimos en la primera la x por lo que vimos en la segunda, quedando algo así:
- (y + 10) + y = 50
Ahora tenemos una ecuación muy simple de una incógnita sola que resolveremos normalmente, obteniendo como resultado:
- 2y = 50 – 10
- 2y = 40
- y = 20
Ya sabes una de las edades, así que ahora usamos este valor en la otra ecuación y la resolvemos nuevamente, quedando un procedimiento similar a este:
- x = (20) + 10
- x = 30
Como ves, el par X=30 e Y=20 verifica las dos ecuaciones dadas al principio.
Método de reducción
Si bien puede ser el más difícil de entender, es también de los más efectivos y útiles para este tipo de sistemas de ecuaciones, además con algo de práctica se vuelve simple.
Para cambiar el ejemplo, utilizaremos el siguiente sistema de ecuaciones:
2x + y = 42
4x – 2y = 36
Lo que haremos será operar en forma inteligente para sumar las ecuaciones o restarlas de modo de despejar alguna de las incógnitas en alguna de las ecuaciones.
En este caso, vamos a necesitar hacer una multiplicación y una suma. En concreto, mutliplicaremos todos los términos de la primera ecuación por 2 y efectuaremos la suma término a término con la segunda ecuación de modo que nos quedarán solo X para despejar.
2x + y = 42 (Todo multiplicado por 2)
4x +2y =84
4x – 2y = 36
——————
8x + 0y = 120
8x = 120
x = 120/8
x = 15
Una vez conocemos el valor de X, utilizamos el método de sustitución para finalizar, tomando cualquiera de las dos ecuaciones y sustituyendo su X por lo que hayamos encontrado, en este caso 15:
2x + y = 42
2 (15) + y = 42
30 + y = 42
y = 42 – 30
y = 12
Método de igualación
Este método consiste en despejar la X en función de Y en ambas ecuaciones y luego igualarlas para saber cuánto vale la segunda incógnita. por ejemplo:
- x + y = 42
- x – y + 22 = 36
Entonces, despejamos y obtenemos:
- x = 42 – y
- x = 36 – 22 + y = 14 + y
Por último:
- 42 – y = 14 + y
- 42 – 14 = y+y
- 28 = 2y
- 28/2 = y
- 14 = y
Luego despejamos la x sustituyendo y listo.
Podría interesarte: Cómo sacar un porcentaje de una cifra, Múltiplos de 3: Cuáles son y cómo se calculan y Múltiplos de 7: Cuáles son y cómo se calculan.
Al fin y al cabo existen distintas formas de resolver ecuaciones de primer grado con dos incógnitas, es cuestión de ir practicándolos para que la resolución de estos problemas sea cada vez más simple. Las ecuaciones se pueden complicar cuando aparecen fracciones (con numeradores y denominadores) que requerirán aplicar técnicas de despeje de fórmula.
También existen aplicaciones de Android para resolver ecuaciones de todo tipo o si prefieres algo más clásico, calculadoras avanzadas que permiten la introducción de incógnitas, aunque lógicamente la misma no interpretará problemas.
¡Recuerda que nada es mejor que evitar posponer las tareas de la escuela o universidad!
