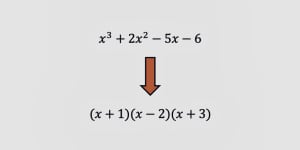
Las raíces de un polinomio son aquellos valores que, si sustituimos la variable "x" por ellos, el resultado de la ecuación del polinomio es cero. Esto, dicho de una forma más coloquial, se puede expresar como los valores de X para los que el polinomio vale cero.
Otra forma que tenemos de pensar en las raíces, es ver que cualquier polinomio puede ser escrito como un producto de binomios del tipo (x - a) donde "x" es una variable y "a" es una raíz. Entonces, un polinomio de tercer grado se escribiría del modo: (x-a).(x-b).(x-c) siendo a, b y c las raíces no necesariamente distintas entre sí.
Para hallar las raíces de un polinomio lo que hay que hacer, entonces, es igualarlo a 0 para averiguar qué valores debe adoptar la variable (generalmente "X") para que la ecuación nos de como resultado 0. Claro está que cuanto mayor sea el grado del polinomio mayor será también la cantidad de pasos que deberemos seguir pues el grado del polinomio nos determina el máximo de raíces distintas que puede tener.
Hallar la raíz de un polinomio de primer grado
Si tenemos un polinomio de primer grado y queremos hallar su raíz, debemos simplemente igualar la ecuación a 0. Realizando los despejes comunes de cualquier ecuación obtendrás un valor para “X” y esa será la raíz de tu polinomio.
Raíces evidentes de cualquier polinomio
Existen algunos casos de polinomios donde se presentan raíces que son evidentes, es decir, que podemos averiguar simplemente mediante la observación y evitando hacer cálculos demasiado trabajosos. Veamos los casos más particulares:
- 0 es raíz cuando el polinomio con el que trabajamos no tiene término independiente. Es decir, cuando todos los términos de nuestro polinomio contienen alguna “x” cualquiera sea su exponente.
- 1 es raíz del polinomio cuando al sumar sus coeficientes obtenemos como resultado 0. Esto quiere decir que si sumas los coeficientes que multiplican a tus “x” y también al término independiente y obtienes 0 como resultado, puedes asegurar que 1 es raíz.
- – 1 es raíz del polinomio cuando la diferencia entre los coeficientes pares y los impares es 0.
Método de Ruffini para polinomios
El método de Ruffini para polinomios nos permite dividir un polinomio de grado 2 o mayor con el fin de obtener uno de un grado menor, para seguir en la búsqueda de las raíces que aún no se conozcan. Sirve mucho en el caso de polinomios de tercer grado, ya que si logramos descifrar alguna de sus raíces podremos obtener uno de grado 2 y finalmente mediante la fórmula de Bhaskara, averiguar las dos raíces restantes.
La aplicación del método de Ruffini en polinomios consiste en utilizar la raíz que conocemos del polinomio para dividirlo. En realidad, si sabemos que “-1” es raíz, entonces el binomio “(x+1)” forma parte del producto de binomios que da como resultado el polinomio, entonces lo que hacemos es dividir al mismo por ese binomio.
La tabla de Ruffini (ver imagen) consiste en colocar la raíz en el costado y, en la parte superior ir introduciendo los coeficientes grado a grado sin saltarse ninguno. Por ejemplo, en caso de ser un polinomio grado 4 que no tenga término de grado 3, en su lugar pondremos un 0.
El primer coeficiente se copia sin sufrir modificaciones en la parte inferior. Luego multiplicamos éste por la raíz y el resultado se coloca en la columna siguiente, en la línea del medio. Posteriormente, realizamos la resta entre los términos de esa columna y obtendremos el resultado que se ubicará en la parte inferior de la misma. Repetimos el procedimiento y, de haber hecho bien los cálculos, en la última columna el resultado de la resta será 0.
Habrás obtenido entonces una serie de números en la parte inferior de cada columna. Pues bien, son los coeficientes de tu nuevo polinomio ordenados de mayor a menor. Ten en cuenta que el de mayor grado tendrá un grado menos que el polinomio que dividiste.
Fórmula de Bhaskara
Si mediante distintos métodos obtuviste un polinomio de segundo grado y quieres saber sus raíces pero no cuentas con ninguna que sea evidente, entonces lo que puedes hacer es recurrir a la fórmula de Bhaskara, que te permitirá averiguar fácilmente cuales son las raíces.
Sabemos que un polinomio de segundo grado se escribe de la siguiente manera:
ax^2 + bx + c = 0
De ahí podrás obtener los valores para sustituir en la fórmula de Bhaskara y finalmente averiguar el valor de las raíces.
Podría interesarte: Cómo sacar un porcentaje de una cifra, Múltiplos de 3: Cuáles son y cómo se calculan y Múltiplos de 7: Cuáles son y cómo se calculan.
Existen variados métodos para calcular las raíces de un polinomio. Con práctica es posible ir aprendiendo todos. Lo importante es tener en claro que cualquier polinomio tiene como máximo el mismo número de raíces que el del exponente de mayor grado del polinomio.
